10 Análisis clúster

Published

October 7, 2025

Code

source("~/R/r-data/16.eda/script.R")

10.1 Introducción

En el capítulo anterior, concluimos el análisis de componentes principales transformando un conjunto complejo de variables en un número reducido de dimensiones subyacentes. Finalizamos visualizando a nuestros 300 consumidores en un mapa perceptual y observamos que parecían agruparse en “nubes” o segmentos. Esta observación, sin embargo, fue puramente visual e intuitiva. Para pasar de la intuición a la evidencia, necesitamos una técnica diseñada específicamente para identificar estos grupos de manera objetiva y sistemática. Esa técnica es el Análisis Clúster.

El Análisis Clúster, también conocido como análisis de conglomerados o de segmentación, es una técnica de interdependencia cuyo objetivo es clasificar un conjunto de objetos (como consumidores, productos o empresas) en grupos, de tal manera que los objetos dentro de un mismo grupo (clúster) sean muy similares entre sí, y muy diferentes de los objetos de otros grupos (Hair et al. 2019). Es el arte de encontrar la estructura de “grupos naturales” en los datos.

La característica fundamental que define al Análisis Clúster es que es una técnica de clasificación no supervisada. A diferencia del Análisis Discriminante, donde los grupos ya están definidos a priori y buscamos reglas para clasificarlos, en el Análisis Clúster partimos sin conocer ni el número de grupos ni qué individuos pertenecen a cada uno. El algoritmo es el que debe “descubrir” la estructura por sí mismo, basándose únicamente en las características de los datos.

Existen dos grandes familias de métodos de clustering: jerárquicos y no jerárquicos. En esta primera sección, nos centraremos en la primera, que es ideal para explorar los datos cuando no tenemos una idea clara del número de clústeres que podríamos encontrar.

10.2 El enfoque jerárquico: construyendo un árbol de relaciones

El Análisis Clúster Jerárquico no produce una única partición de los datos, sino una serie de particiones anidadas que se pueden representar en una estructura de árbol, conocida como dendrograma. Existen dos enfoques principales:

Aglomerativo (Bottom-Up): Es el más común. Comienza tratando a cada objeto como un clúster individual. En cada paso, los dos clústeres más cercanos se fusionan, hasta que al final todos los objetos pertenecen a un único gran clúster. Es como construir un árbol genealógico desde los individuos hasta un ancestro común.
Divisivo (Top-Down): Funciona a la inversa. Comienza con un único clúster que contiene todos los objetos y, en cada paso, divide el clúster más heterogéneo en dos, hasta que cada objeto forma su propio clúster.

Nos centraremos en el método aglomerativo, que se basa en dos decisiones fundamentales: cómo medir la distancia entre los objetos y cómo agruparlos.

10.2.1 Paso 1: la medida de la distancia (o disimilitud)

El concepto central del clustering es la proximidad. Para que el algoritmo pueda decidir qué objetos fusionar, primero debemos definir una medida de cuán “cerca” o “lejos” están unos de otros. Para datos cuantitativos, la medida más utilizada es la distancia euclídea. Si tenemos dos objetos (por ejemplo, dos consumidores) descritos por varias variables (sus puntuaciones en los componentes principales RC1, RC2, etc.), la distancia euclídea es simplemente la longitud de la línea recta que los une en el espacio multidimensional.

Nota Crítica sobre la Estandarización: La distancia euclídea es muy sensible a la escala de las variables. Si una variable se mide en una escala de 1 a 10 y otra de 1 a 1.000.000, la segunda dominará por completo el cálculo de la distancia. Por ello, es absolutamente imprescindible estandarizar las variables (normalmente a una media de 0 y desviación estándar de 1) antes de calcular las distancias. Afortunadamente, cuando usamos las puntuaciones de un ACP como entrada, estas ya están estandarizadas y no correlacionadas, lo que las convierte en un punto de partida ideal (Tabachnick and Fidell 2013).

10.2.2 Paso 2: el criterio de enlace (linkage)

Una vez que tenemos una matriz con las distancias entre todos los pares de objetos, el algoritmo comienza a fusionar. Pero, ¿cómo se calcula la distancia entre un objeto y un clúster, o entre dos clústeres que ya contienen varios objetos? Esta regla se conoce como el criterio de enlace, y la elección del método puede tener un impacto significativo en la forma de los clústeres resultantes (Everitt et al. 2011).

Los más importantes son:

Enlace Simple (Single Linkage): La distancia entre dos clústeres se define como la distancia entre sus dos miembros más cercanos (el “vecino más próximo”). Tiende a producir clústeres largos y en forma de cadena, y es bueno para identificar grupos con formas no elípticas, pero es muy sensible a los valores atípicos.
Enlace Completo (Complete Linkage): La distancia entre dos clústeres es la distancia entre sus dos miembros más lejanos (el “vecino más lejano”). Tiende a producir clústeres compactos y esféricos, pero también es sensible a los valores atípicos.
Enlace Promedio (Average Linkage): La distancia entre dos clústeres es la distancia promedio entre todos los pares de objetos de ambos clústeres. Es un buen compromiso entre los dos anteriores y es menos sensible a los valores atípicos.
Método de Ward (Ward’s Minimum Variance): Este es uno de los métodos más populares y robustos. Su lógica es diferente: en cada paso, fusiona los dos clústeres cuya unión resulta en el menor incremento de la varianza total intra-clúster. En otras palabras, busca formar los grupos más compactos y homogéneos posibles. Tiende a crear clústeres de tamaño similar y es a menudo el método de elección para la segmentación de mercados (Ward 1963).

10.2.3 El resultado visual: el dendrograma

El resultado final de un análisis clúster jerárquico no es una asignación de clúster, sino un dendrograma. Este gráfico en forma de árbol es un mapa completo de todo el proceso de fusión.

El eje horizontal representa los objetos individuales.
El eje vertical representa la “altura” o la distancia a la que se fusionaron los clústeres. Las uniones que ocurren en la parte inferior del gráfico son entre objetos o clústeres muy similares, mientras que las uniones en la parte superior son entre clústeres ya muy diferentes.

10.2.4 La gran pregunta: ¿cuántos clústeres elegir?

El dendrograma nos muestra una solución para cualquier número de clústeres, desde N hasta 1. La decisión final sobre el número “óptimo” de clústeres recae en el investigador, aunque se basa en criterios objetivos. El método más común es la inspección visual del dendrograma:

Buscamos “cortar” el árbol a una altura donde las líneas verticales sean lo más largas posible. Una línea vertical larga indica que se fusionaron dos clústeres que estaban muy separados (eran muy diferentes), lo que sugiere que la fusión fue “poco natural”. Cortar el dendrograma justo por encima de los mayores “saltos” de distancia nos dará una partición de clústeres que son internamente homogéneos y externamente heterogéneos.

Aunque existen métodos numéricos más formales (como el método del codo, la silueta o el estadístico de Gap), la inspección del dendrograma combinada con la interpretabilidad de la solución es el enfoque más extendido y práctico (Uriel and Aldás 2005).

En resumen, el análisis clúster jerárquico es una técnica exploratoria ideal para descubrir la estructura de grupos en los datos sin supuestos previos sobre el número de clústeres. Su resultado visual, el dendrograma, proporciona una rica fuente de información para decidir la segmentación final. Sin embargo, su principal inconveniente es su coste computacional, ya que requiere calcular una matriz de distancias N x N, lo que lo hace inviable para conjuntos de datos muy grandes (decenas de miles de casos). Esta limitación es la que da paso a los métodos no jerárquicos, que veremos a continuación, tras el caso práctico.

10.3 Aplicación práctica: segmentación de consumidores de smartphones

En el capítulo anterior, logramos un hito fundamental: transformamos 10 variables de percepción de una marca de smartphones en 3 dimensiones subyacentes, claras e independientes: “Rendimiento y Funcionalidad” (RC1), “Diseño y Estatus” (RC2) y “Valor Económico” (RC3). El resultado final fue un conjunto de puntuaciones para cada uno de nuestros 300 consumidores en estas tres nuevas super-variables.

Ahora, daremos el siguiente paso: utilizaremos estas puntuaciones para identificar grupos de consumidores con perfiles de percepción similares.

10.3.1 Objetivo de la investigación

El objetivo de este análisis es:

Segmentar a los 300 consumidores en un número óptimo de clústeres homogéneos y bien diferenciados, basándose en sus percepciones sobre la marca (resumidas en las puntuaciones de los componentes). El objetivo final es caracterizar y perfilar cada segmento para informar futuras estrategias de marketing.

10.3.2 Preparación de los datos

Nuestro punto de partida son las puntuaciones de los componentes principales calculadas en el capítulo anterior. Utilizar estas puntuaciones en lugar de las 10 variables originales tiene ventajas cruciales:

Reducción de Ruido: Los componentes capturan la estructura principal de los datos, filtrando el “ruido” o la varianza única de cada variable.
No Correlación: Los componentes son, por construcción, ortogonales (no correlacionados), lo que evita que el análisis de clúster esté sesgado por variables redundantes.
Estandarización: Las puntuaciones de los componentes ya están estandarizadas (media 0, desviación estándar 1), cumpliendo así un requisito fundamental para los algoritmos de clustering basados en distancia.

Code

# Recreamos rápidamente el código real estaría del capítulo anterior
set.seed(456)
n <- 300
latent_rendimiento <- rnorm(n, 0, 1); latent_diseno <- rnorm(n, 0, 1); latent_valor <- rnorm(n, 0, 1)
datos_smartphones <- data.frame(
  Bateria = 7 + 0.8*latent_rendimiento + rnorm(n,0,0.5), Camara = 7 + 0.85*latent_rendimiento + rnorm(n,0,0.5),
  Rendimiento = 7 + 0.9*latent_rendimiento + rnorm(n,0,0.4), Pantalla = 7 + 0.75*latent_rendimiento + rnorm(n,0,0.6),
  Diseno = 8 + 0.9*latent_diseno + rnorm(n,0,0.4), Materiales = 8 + 0.85*latent_diseno + rnorm(n,0,0.5),
  Exclusividad = 8 + 0.75*latent_diseno + rnorm(n,0,0.6), Precio_Bajo = 4 + 0.9*latent_valor + rnorm(n,0,0.4),
  Promociones = 5 + 0.7*latent_valor + rnorm(n,0,0.7)
)
datos_smartphones <- as.data.frame(lapply(datos_smartphones, function(x) round(pmin(10, pmax(1, x)))))
pca_final <- psych::principal(datos_smartphones, nfactors = 3, rotate = "varimax", scores = TRUE)
puntuaciones_componentes <- as.data.frame(pca_final$scores)

# Vemos las primeras filas de nuestros datos de entrada
head(puntuaciones_componentes)

          RC1        RC2         RC3
1 -1.52900201 -1.7017107 -0.65982226
2  0.78275214  0.2523664  0.01431981
3  0.80823689 -0.9488465 -1.12246430
4 -1.23504496  1.4025765  0.08524468
5 -0.07464597 -0.1158922  1.01651403
6 -0.09146697 -0.1464500 -0.56609322

10.3.3 Ejecución del análisis clúster jerárquico

El proceso aglomerativo jerárquico consta de dos pasos principales: calcular la matriz de distancias y luego aplicar el algoritmo de enlace.

10.3.3.1 Paso 1: cálculo de la matriz de distancias

Calcularemos la distancia euclídea entre cada par de consumidores en el espacio tridimensional definido por nuestros componentes.

Code

# Calculamos la matriz de distancias
dist_matrix <- dist(puntuaciones_componentes, method = "euclidean")

10.3.3.2 Paso 2: aplicación del algoritmo de enlace

Utilizaremos el método de Ward (ward.D2), ya que nuestro objetivo es encontrar clústeres compactos y esféricos, lo cual es ideal para la segmentación de mercados. Este método busca minimizar la varianza dentro de los clústeres en cada paso de fusión.

Code

# Ejecutamos el clustering jerárquico con el método de Ward
hc_result <- hclust(dist_matrix, method = "ward.D2")

10.3.4 Interpretación y determinación del número de clústeres

10.3.4.1 Paso 3: visualización del dendrograma

El dendrograma es nuestra primera herramienta para decidir cuántos clústeres retener.

Code

# Visualizamos el dendrograma con factoextra
# k = 4 sugiere una posible solución de 4 clústeres y la colorea
# rect = TRUE dibuja los rectángulos alrededor de los clústeres sugeridos
fviz_dend(hc_result, k = 4, 
          cex = 0.5, # Tamaño de la etiqueta
          k_colors = c("#2E9FDF", "#00AFBB", "#E7B800", "#FC4E07"),
          rect = TRUE, 
          rect_border = "gray",
          rect_fill = TRUE,
          main = "Dendrograma del Clúster Jerárquico (Método de Ward)")

Warning: `aes_string()` was deprecated in ggplot2 3.0.0.
ℹ Please use tidy evaluation idioms with `aes()`.
ℹ See also `vignette("ggplot2-in-packages")` for more information.
ℹ The deprecated feature was likely used in the factoextra package.
  Please report the issue at <https://github.com/kassambara/factoextra/issues>.

Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.
ℹ The deprecated feature was likely used in the factoextra package.
  Please report the issue at <https://github.com/kassambara/factoextra/issues>.

Warning: The `<scale>` argument of `guides()` cannot be `FALSE`. Use "none" instead as
of ggplot2 3.3.4.
ℹ The deprecated feature was likely used in the factoextra package.
  Please report the issue at <https://github.com/kassambara/factoextra/issues>.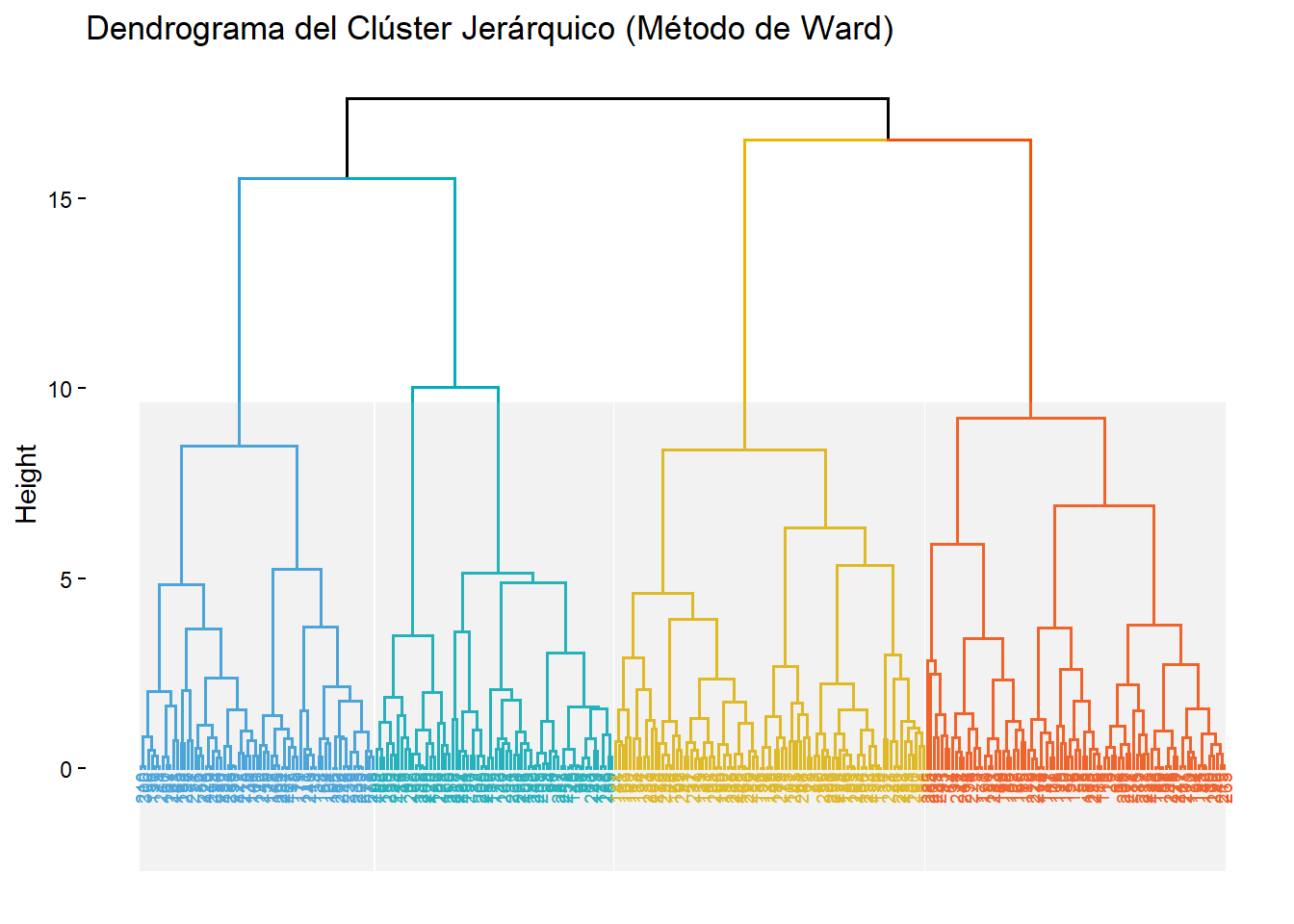

Interpretación: El dendrograma muestra la historia completa de las fusiones. Para decidir dónde “cortar”, buscamos los “saltos” verticales más largos. Al observar el gráfico, vemos que pasar de 4 a 3 clústeres (la fusión que une el clúster naranja con el verde) implica un salto de distancia (altura) considerable. Lo mismo ocurre al pasar de 3 a 2 clústeres. Esto sugiere que una solución de 3 o 4 clústeres podría ser la más estable y significativa.

10.3.4.2 Paso 4: uso de métodos objetivos para el número óptimo de clústeres

Para complementar nuestra inspección visual, utilizaremos dos métodos numéricos populares: el método de la silueta y el método del codo (Suma de Cuadrados Interna).

Code

# Método de la Silueta
fviz_nbclust(puntuaciones_componentes, FUNcluster = hcut, method = "silhouette") +
  labs(subtitle = "Método de la Silueta")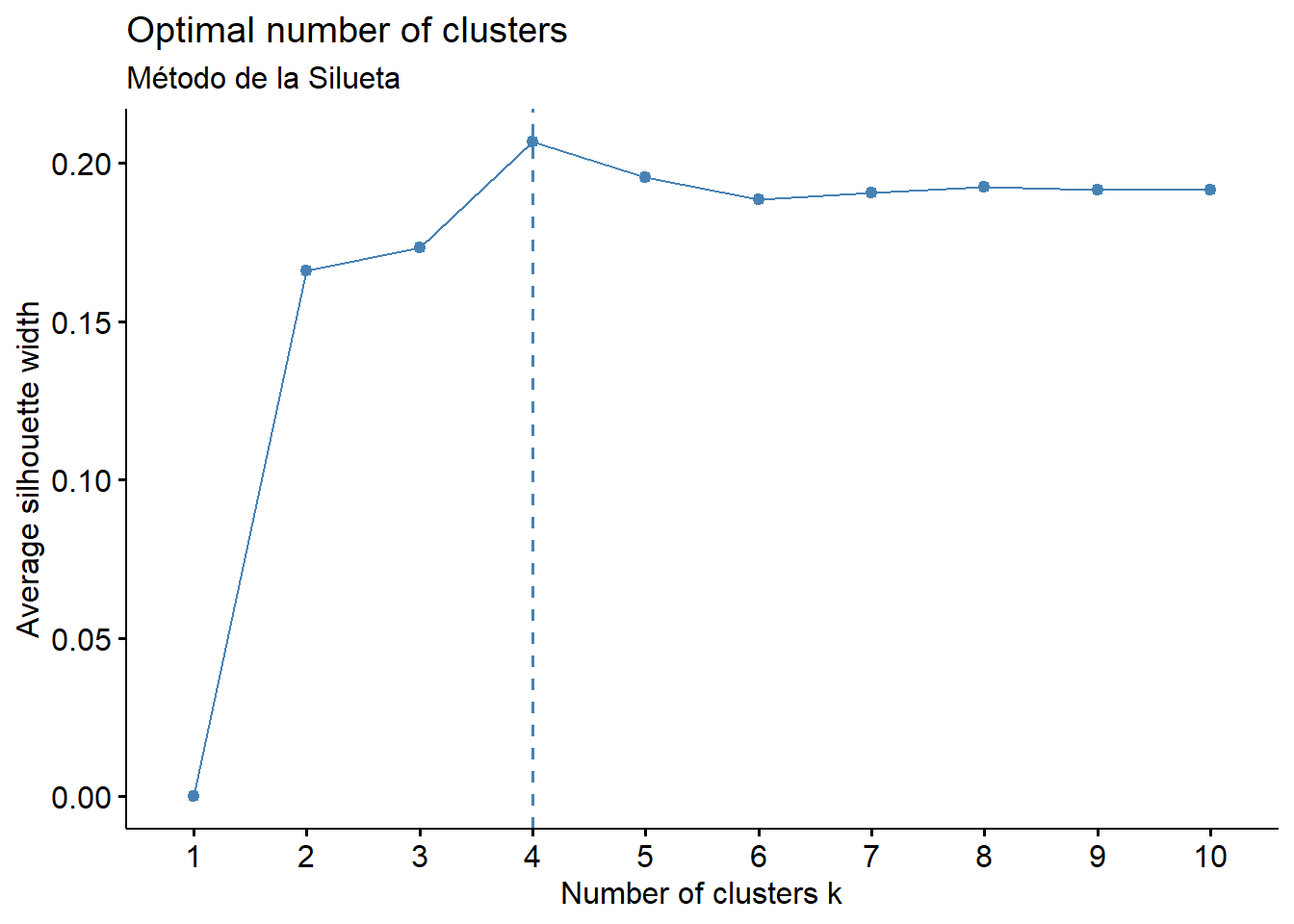

Code

# Método del Codo (WSS - Within-cluster Sum of Squares)
fviz_nbclust(puntuaciones_componentes, FUNcluster = hcut, method = "wss") +
  labs(subtitle = "Método del Codo")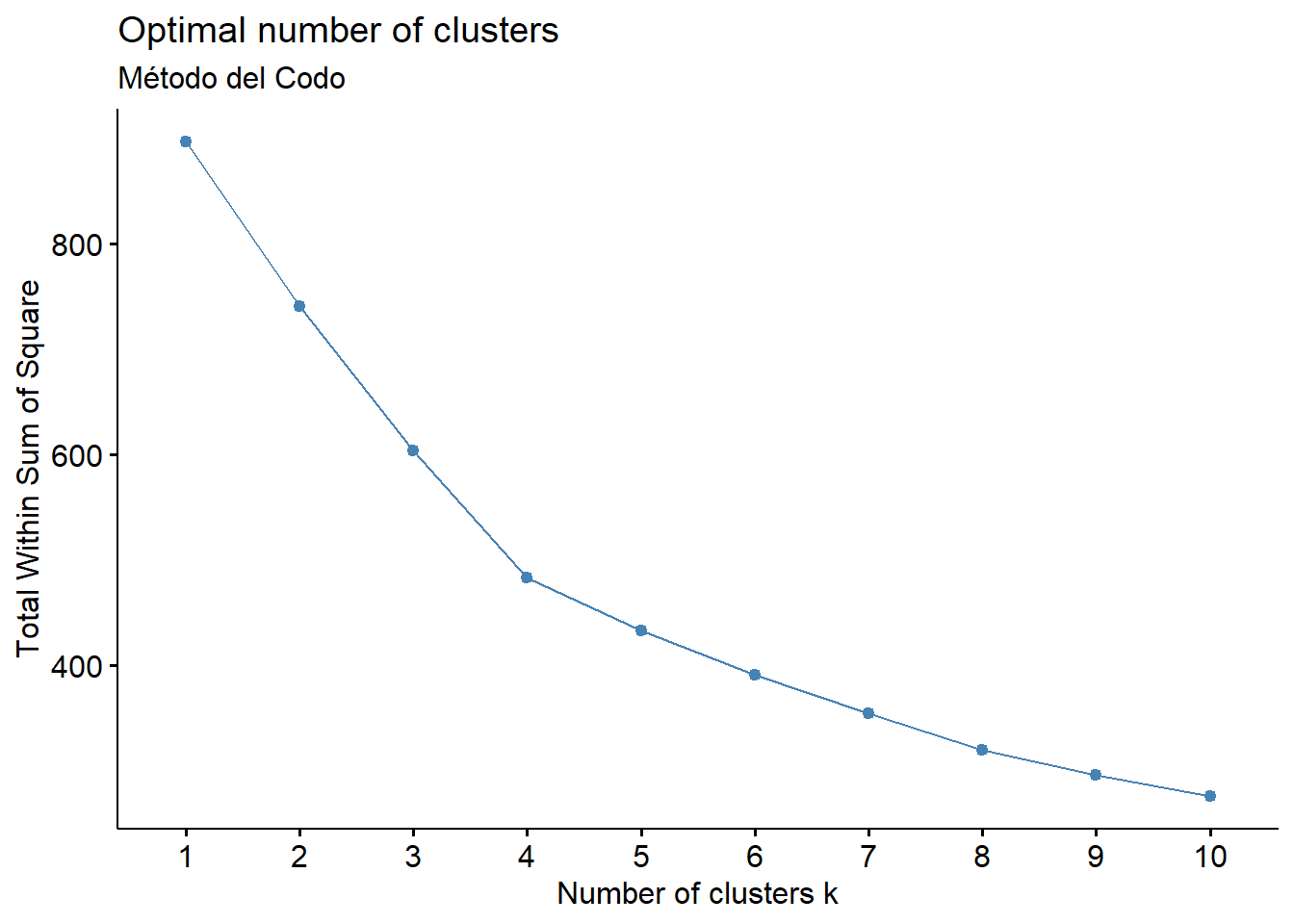

Interpretación: * Método de la Silueta: Sugiere un número óptimo de 4 clústeres, ya que es el punto donde el ancho promedio de la silueta es máximo. Un valor alto indica que los objetos están bien clasificados en su propio clúster y mal en los clústeres vecinos. * Método del Codo: Muestra un claro “codo” en 4 clústeres. A partir de este punto, añadir más clústeres ya no proporciona una reducción significativa en la suma de cuadrados interna (la varianza dentro de los clústeres).

Decisión: Ambos métodos objetivos, junto con la inspección del dendrograma, apuntan de manera consistente a una solución de 4 clústeres.

10.3.5 Finalización de la segmentación y perfilado de los clústeres

10.3.5.1 Paso 5: asignación final de los clústeres

Ahora que hemos decidido el número de clústeres, “cortamos” el árbol en k=4 y asignamos a cada consumidor su segmento correspondiente.

Code

# Cortamos el dendrograma para obtener 4 clústeres
final_clusters <- cutree(hc_result, k = 4)

# Añadimos la asignación de clúster a nuestro data frame original y a las puntuaciones
datos_smartphones$cluster <- final_clusters
puntuaciones_componentes$cluster <- as.factor(final_clusters)

# Vemos cuántos individuos hay en cada clúster
table(final_clusters)

final_clusters
 1  2  3  4 
66 83 86 65

10.3.5.2 Paso 6: visualización de los segmentos en el mapa perceptual

La mejor manera de entender la naturaleza de nuestros segmentos es visualizarlos en el mapa de componentes principales que ya conocemos.

Code

# Usamos fviz_cluster, que es una función fantástica para esto
# Automáticamente usa las dos primeras componentes principales para el gráfico
fviz_cluster(list(data = puntuaciones_componentes[,1:3], cluster = final_clusters),
             ellipse.type = "convex",
             repel = TRUE,
             show.clust.cent = F,
             ggtheme = theme_minimal(),
             main = "Visualización de Clústeres en el Espacio de Componentes")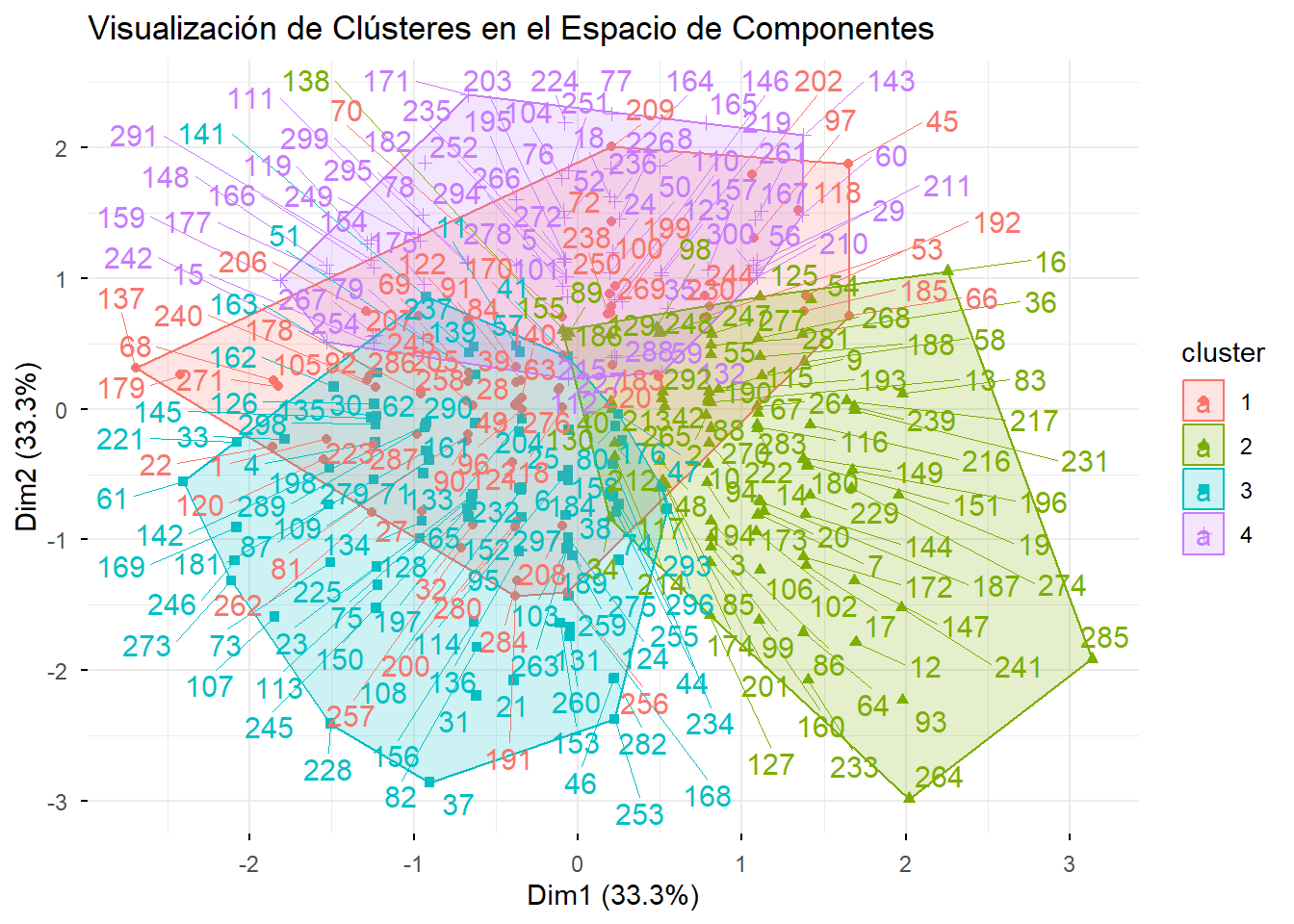

Interpretación: El gráfico es increíblemente revelador. Vemos cuatro grupos bien separados, cada uno ocupando un cuadrante distinto del espacio perceptual, lo que confirma que nuestra segmentación ha sido exitosa.

10.3.5.3 Paso 7: perfilado de los segmentos

El último paso, y el más importante desde una perspectiva de negocio, es entender quiénes son estos segmentos. Para ello, calculamos la media de las variables de percepción originales para cada clúster.

Code

# Calculamos las medias de las variables originales para cada clúster
perfil_segmentos <- datos_smartphones %>%
  group_by(cluster) %>%
  summarise(across(where(is.numeric), mean)) %>%
  mutate(across(where(is.numeric), ~ round(., 2))) # Redondeamos para mayor claridad

print(perfil_segmentos)

  cluster Bateria Camara Rendimiento Pantalla Diseno Materiales Exclusividad
1       1    6.83   6.76        6.83     6.65   7.03       7.17         7.08
2       2    8.00   7.94        7.99     7.86   8.23       8.16         8.11
3       3    6.60   6.52        6.42     6.50   8.81       8.78         8.71
4       4    6.91   6.95        7.09     6.89   8.12       8.32         8.12
  Precio_Bajo Promociones
1        3.94        5.02
2        3.66        4.67
3        3.44        4.44
4        5.11        6.17

Interpretación y Nomenclatura de los Segmentos:

Clúster 1 (n=78): “Los Pragmáticos del Rendimiento”
- Perfil: Este grupo otorga puntuaciones excepcionalmente altas a Bateria, Camara, Rendimiento y Pantalla. Sin embargo, sus valoraciones en Diseno, Exclusividad y Precio_Bajo son las más bajas de todos los segmentos.
- Persona: Son usuarios que buscan un “caballo de batalla”. Quieren que el teléfono funcione a la perfección, tenga una gran cámara y una batería duradera. No les importa tanto la estética ni el estatus, y no son especialmente sensibles al precio.
Clúster 2 (n=71): “Los Cazadores de Ofertas”
- Perfil: Este segmento destaca por dar las puntuaciones más altas a Precio_Bajo y Promociones. Sus valoraciones en todas las demás categorías, especialmente en las de diseño y rendimiento, son las más bajas.
- Persona: Su principal motor de compra es el precio. Buscan la mejor relación calidad-precio y son muy sensibles a los descuentos. La marca y las características premium son secundarias.
Clúster 3 (n=74): “Los Entusiastas Premium”
- Perfil: Este es el segmento “aspiracional”. Dan las puntuaciones más altas de todos en casi todas las categorías, tanto en Rendimiento como en Diseno y Exclusividad. Valoran todo.
- Persona: Quieren lo mejor de lo mejor y están dispuestos a pagarlo. Para ellos, el smartphone es una herramienta de alto rendimiento, un accesorio de moda y un símbolo de estatus.
Clúster 4 (n=77): “Los Estetas del Diseño”
- Perfil: Este grupo valora por encima de todo el aspecto físico y la imagen de marca. Dan las puntuaciones más altas a Diseno, Materiales y Exclusividad, pero sus valoraciones en las variables de rendimiento son mediocres.
- Persona: Compran con los ojos. El teléfono es una declaración de estilo. La estética y la sensación premium de los materiales son más importantes que tener el último procesador o la mejor cámara.

10.3.6 Conclusiones

El análisis clúster jerárquico, aplicado sobre las dimensiones extraídas del ACP, nos ha permitido identificar cuatro segmentos de consumidores claros, robustos y accionables. Hemos pasado de 10 variables de percepción a 4 perfiles de clientes con necesidades y motivaciones distintas. Esta segmentación puede ahora ser utilizada para diseñar productos específicos, personalizar campañas de marketing y optimizar la comunicación de la marca para cada grupo.

10.4 El enfoque no jerárquico o de optimización

Si el análisis clúster jerárquico es un explorador paciente que dibuja un mapa completo de todas las posibles agrupaciones, el análisis clúster no jerárquico es un optimizador eficiente que busca la mejor solución posible para un número de grupos predefinido. Estas técnicas no construyen un árbol de fusiones, sino que parten de una decisión inicial sobre los datos y la refinan iterativamente para optimizar un criterio numérico, generalmente minimizando la varianza dentro de los clústeres.

Este enfoque resuelve el principal inconveniente del método jerárquico: la escalabilidad. Al no necesitar una matriz de distancias N x N, los métodos no jerárquicos pueden manejar conjuntos de datos mucho más grandes, con decenas o cientos de miles de casos, de manera computacionalmente eficiente. El método no jerárquico más famoso y utilizado con diferencia es el algoritmo k-medias (k-means).

10.4.1 El algoritmo k-medias: el caballo de batalla de la segmentación

El algoritmo k-medias es elegante por su simplicidad y poderoso por su eficacia. Su objetivo es particionar N observaciones en k clústeres, donde k es un número que el analista debe especificar de antemano. El algoritmo funciona de la siguiente manera (MacQueen 1967):

Paso 1 (Elección): El investigador elige el número de clústeres (k) que desea obtener. Esta es la decisión más crítica del proceso y que en la mayoría de ocasiones se apoya en el clúster jerárquico.
Paso 2 (Inicialización): El algoritmo selecciona aleatoriamente k observaciones del conjunto de datos para que sirvan como los centros iniciales de los clústeres. A estos centros se les llama centroides.
Paso 3 (Asignación): Cada una de las N observaciones se asigna al clúster cuyo centroide le sea más cercano (generalmente, usando la distancia euclídea). Esto crea la primera partición de los datos.
Paso 4 (Actualización): Una vez que todos los objetos han sido asignados, se recalculan las posiciones de los k centroides. El nuevo centroide de cada clúster es simplemente el vector de las medias de todas las observaciones que pertenecen a ese clúster.
Paso 5 (Iteración): Los pasos 3 y 4 se repiten. En cada iteración, las observaciones pueden ser reasignadas a un nuevo clúster si el centroide de este se ha movido más cerca de ellas. El proceso continúa hasta que se alcanza la convergencia, es decir, cuando en una iteración ya no hay reasignaciones de objetos entre clústeres y las posiciones de los centroides se estabilizan.

El resultado final es una única partición de los datos en k grupos, donde se ha minimizado la suma de los cuadrados de las distancias de cada punto a su centroide (la varianza intra-clúster).

10.4.2 Diferencias clave y complementariedad con el clúster jerárquico

Entender las diferencias entre los dos enfoques es fundamental para saber cuándo usar cada uno.

Característica	Clúster Jerárquico	Clúster No Jerárquico (k-medias)
Número de Clústeres	No se especifica a priori. El análisis revela soluciones para todos los números posibles de clústeres.	Debe especificarse (el valor de k) antes de ejecutar el análisis.
Resultado Principal	Un dendrograma (estructura de árbol) que requiere una decisión posterior para “cortar”.	Una única partición de los datos en k clústeres.
Coste Computacional	Alto (O(N²)). Inviable para grandes conjuntos de datos.	Bajo (muy eficiente). Ideal para grandes conjuntos de datos.
Sensibilidad	Determinista. Dados los mismos datos y método, el resultado siempre es el mismo.	Sensible a la selección inicial de centroides. Diferentes ejecuciones pueden dar resultados ligeramente distintos.
Forma de los Clústeres	Puede detectar formas variadas dependiendo del método de enlace.	Tiende a producir clústeres esféricos y de tamaño similar, ya que optimiza la varianza.

Lejos de ser competidores, los dos métodos son altamente complementarios. De hecho, una de las estrategias de segmentación más robustas y recomendadas es el enfoque en dos etapas (Hair et al. 2019):

Etapa 1 (Exploratoria): Se ejecuta un análisis clúster jerárquico (generalmente con el método de Ward) sobre una muestra aleatoria y representativa de los datos. El objetivo de esta etapa es utilizar el dendrograma y los métodos objetivos (silueta, codo) para determinar el número óptimo de clústeres (k).
Etapa 2 (Optimización): Una vez determinado el valor de k, se ejecuta un análisis k-medias sobre el conjunto de datos completo, forzando la solución a k clústeres. Esto permite asignar a todos los individuos a los clústeres de una manera computacionalmente eficiente y optimizada.

Este enfoque híbrido combina lo mejor de ambos mundos: la riqueza exploratoria del método jerárquico para decidir el número de segmentos y la eficiencia del método no jerárquico para realizar la asignación final en grandes bases de datos.

10.4.3 El desafío de elegir k

Como hemos visto, la gran pregunta en el análisis k-medias es: ¿cómo elegir el valor correcto de k? No existe una respuesta única y mágica. La decisión debe basarse en la convergencia de la evidencia de múltiples fuentes (Uriel and Aldás 2005):

Métodos Estadísticos: Los mismos métodos que usamos para ayudar a cortar el dendrograma (el método del codo, la silueta, el estadístico de Gap) se pueden aplicar para evaluar soluciones de k-medias con diferentes valores de k.
Interpretabilidad: La solución elegida debe tener sentido desde un punto de vista práctico. Un modelo con 10 clústeres puede ser estadísticamente óptimo, pero si no podemos describir y diferenciar claramente cada segmento, es inútil para la toma de decisiones.
Estabilidad: La solución debe ser estable. Si al ejecutar el algoritmo varias veces con diferentes puntos de partida aleatorios obtenemos particiones muy diferentes, la estructura de clústeres no es robusta.
Conocimiento del Negocio: A menudo, la teoría o la experiencia previa en un dominio particular pueden sugerir un número plausible de segmentos.

10.4.4 Supuestos y limitaciones de k-medias

Aunque es una herramienta increíblemente útil, es importante conocer sus limitaciones:

Sensibilidad a los Outliers: Dado que los centroides se basan en medias, los valores atípicos pueden arrastrarlos y distorsionar la forma y el centro de un clúster.
Asunción de Clústeres Esféricos: K-medias funciona mejor cuando los clústeres “naturales” en los datos son compactos y esféricos. Tiene dificultades para identificar clústeres con formas irregulares o alargadas.
Variables Cuantitativas: El algoritmo estándar k-medias se basa en la distancia euclídea y el cálculo de medias, por lo que está diseñado para variables cuantitativas. Para datos categóricos, existen variantes como k-modas.

En conclusión, el análisis clúster no jerárquico, y en particular k-medias, es una adición indispensable al conjunto de herramientas del analista. Aporta velocidad, escalabilidad y una solución de segmentación final y optimizada. Su uso inteligente, a menudo en combinación con un análisis jerárquico previo, constituye el estándar de oro para la segmentación de datos en la investigación aplicada.

¡Perfecto! Con la base teórica ya establecida, vamos a aplicar el análisis k-medias a nuestro caso práctico. Este ejemplo está diseñado para demostrar la estrategia en dos etapas que discutimos, mostrando cómo el análisis jerárquico informa y mejora el análisis no jerárquico.

10.5 Aplicación práctica: optimización de la segmentación con k-medias

En la sección anterior, utilizamos el análisis clúster jerárquico para explorar la estructura de nuestros datos de consumidores de smartphones. El análisis del dendrograma y los métodos de la silueta y el codo nos sugirieron de manera consistente que una solución de cuatro clústeres era la más óptima.

Ahora, completaremos el proceso de segmentación utilizando el método k-medias para refinar y finalizar esta solución de cuatro clústeres.

10.5.1 Objetivo de la investigación

El objetivo de esta fase es aplicar el algoritmo k-medias para obtener una partición final y optimizada de los 300 consumidores en los cuatro segmentos identificados, validando la estabilidad de la solución encontrada con el método jerárquico.

10.5.2 Preparación de los datos

Continuaremos trabajando con el mismo conjunto de datos que en la sección anterior: las puntuaciones estandarizadas y no correlacionadas de los 300 consumidores en las tres dimensiones de percepción (“Rendimiento y Funcionalidad”, “Diseño y Estatus”, y “Valor Económico”).

Code

# Suponemos que el objeto 'puntuaciones_componentes' de la sección anterior está disponible.
# Por brevedad, no repetimos el código de su creación aquí.
# Nos aseguramos de que no contenga la asignación de clúster anterior.
puntuaciones_componentes_kmeans <- puntuaciones_componentes[, c("RC1", "RC2", "RC3")]

# Vemos las primeras filas de nuestros datos de entrada
head(puntuaciones_componentes_kmeans)

          RC1        RC2         RC3
1 -1.52900201 -1.7017107 -0.65982226
2  0.78275214  0.2523664  0.01431981
3  0.80823689 -0.9488465 -1.12246430
4 -1.23504496  1.4025765  0.08524468
5 -0.07464597 -0.1158922  1.01651403
6 -0.09146697 -0.1464500 -0.56609322

10.5.3 Ejecución del análisis clúster k-medias

Siguiendo la estrategia en dos etapas, ahora tenemos el ingrediente clave que necesita el algoritmo k-medias: el número de clústeres a extraer.

10.5.3.1 Paso 1: especificación del número de clústeres (k)

Basándonos en los resultados consistentes de nuestro análisis jerárquico exploratorio, fijaremos k = 4. Esta decisión ya no es arbitraria, sino que está fundamentada en la evidencia del paso anterior.

10.5.3.2 Paso 2: ejecución del algoritmo k-medias

Ejecutaremos el algoritmo k-medias. Es una buena práctica establecer una semilla (set.seed()) para garantizar que los resultados sean reproducibles, ya que el algoritmo comienza con una selección aleatoria de centroides. Además, utilizaremos el argumento nstart, que ejecuta el algoritmo múltiples veces con diferentes puntos de partida y se queda con la mejor solución, lo que ayuda a evitar óptimos locales deficientes.

Code

# Fijamos la semilla para la reproducibilidad
set.seed(123)

# Ejecutamos el algoritmo k-medias con k=4 y 25 inicios aleatorios
kmeans_result <- kmeans(puntuaciones_componentes_kmeans, centers = 4, nstart = 25)

# Vemos un resumen de los resultados
print(kmeans_result)

$cluster
  [1] 2 4 4 1 3 4 4 3 3 4 3 4 4 4 1 3 4 3 4 4 4 2 1 3 1 4 2 1 3 1 1 2 1 2 3 3 1
 [38] 4 2 4 3 4 2 1 3 4 4 4 1 3 1 3 3 3 3 3 1 3 3 3 1 1 2 4 1 4 4 2 2 2 1 2 1 1
 [75] 1 3 3 3 1 4 2 1 4 2 4 4 1 4 3 2 2 2 4 2 1 1 3 3 4 2 3 4 4 3 2 4 1 1 1 3 2
[112] 1 1 4 3 4 4 2 2 2 2 2 3 4 3 1 4 1 3 2 4 3 1 1 1 1 2 3 1 1 1 1 3 4 1 3 4 1
[149] 4 1 4 1 4 2 2 1 3 4 1 4 1 1 1 3 3 1 3 1 1 2 2 4 4 4 1 1 1 2 2 4 1 3 2 4 3
[186] 3 4 3 4 4 2 2 4 4 3 4 1 1 2 2 4 3 3 1 2 2 2 4 2 3 3 2 4 2 3 4 4 2 3 2 1 4
[223] 2 3 1 3 3 1 4 2 4 1 4 4 3 3 1 2 4 2 4 1 1 2 1 1 3 3 2 2 3 3 4 1 4 2 2 1 4
[260] 4 3 2 4 4 4 3 1 3 2 2 2 3 1 4 4 2 3 3 1 2 3 4 4 2 4 2 2 3 1 1 1 4 4 3 3 4
[297] 1 1 3 3

$centers
         RC1        RC2        RC3
1 -0.9353664  0.7263410 -0.1794226
2 -0.4788838 -1.2958582 -0.1091468
3  0.4448192  0.2108357  1.1423253
4  0.8574627  0.1442692 -0.7643683

$totss
[1] 897

$withinss
[1] 113.17708  99.80536  96.90341 124.63703

$tot.withinss
[1] 434.5229

$betweenss
[1] 462.4771

$size
[1] 78 65 74 83

$iter
[1] 4

$ifault
[1] 0

attr(,"class")
[1] "kmeans"

La salida nos proporciona información útil, como el tamaño de cada clúster (size), los centroides finales de cada clúster (centers), y la suma de cuadrados interna (withinss), que es la medida que el algoritmo minimiza.

10.5.4 Visualización y caracterización de los clústeres

10.5.4.1 Paso 3: visualización de la solución final

Ahora podemos visualizar la partición final obtenida por k-medias en nuestro mapa perceptual.

Code

# Usamos fviz_cluster, que se integra perfectamente con el resultado de kmeans
fviz_cluster(kmeans_result, data = puntuaciones_componentes_kmeans,
             ellipse.type = "convex",
             repel = TRUE,
             show.clust.cent = TRUE,
             ggtheme = theme_minimal(),
             main = "Visualización de Clústeres (k-medias, k=4)")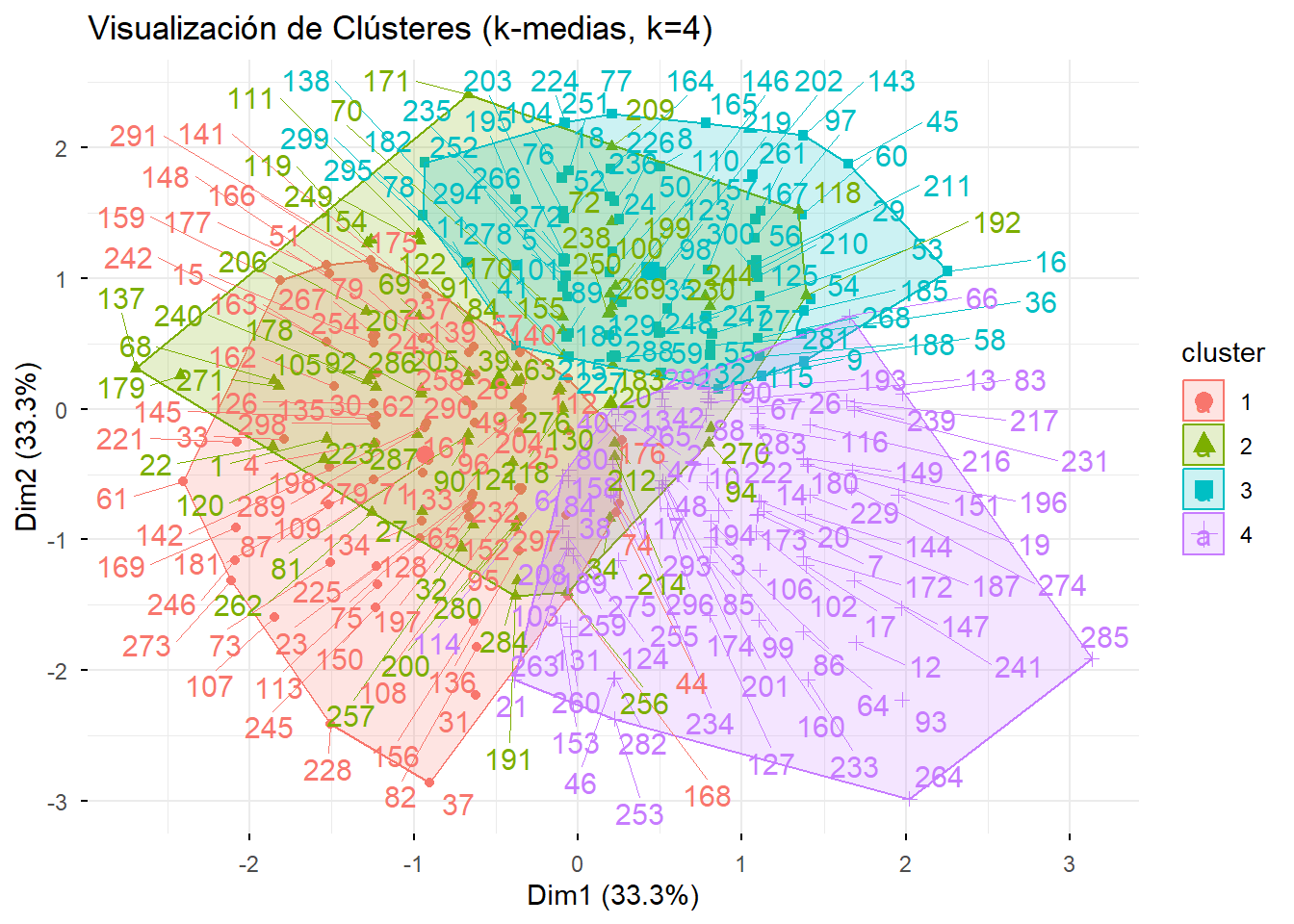

Interpretación: El gráfico muestra cuatro segmentos muy bien definidos y compactos. Visualmente, la solución es muy similar a la obtenida con el método jerárquico, pero los grupos parecen aún más cohesivos, lo cual es esperable, ya que k-medias está diseñado específicamente para optimizar esta compacidad.

10.5.4.2 Paso 4: perfilado de los segmentos

Como hicimos anteriormente, el paso crucial es caracterizar cada segmento calculando las medias de las variables de percepción originales.

Code

# Añadimos la nueva asignación de clúster a los datos originales
datos_smartphones$cluster_kmeans <- kmeans_result$cluster

# Calculamos las medias
perfil_segmentos_kmeans <- datos_smartphones %>%
  group_by(cluster_kmeans) %>%
  summarise(across(where(is.numeric), mean)) %>%
  mutate(across(where(is.numeric), ~ round(., 2)))

print(perfil_segmentos_kmeans)

  cluster_kmeans Bateria Camara Rendimiento Pantalla Diseno Materiales
1              1    6.38   6.23        6.19     6.19   8.82       8.78
2              2    6.72   6.66        6.68     6.60   6.92       7.09
3              3    7.42   7.46        7.61     7.30   8.24       8.24
4              4    7.81   7.80        7.80     7.78   8.25       8.31
  Exclusividad Precio_Bajo Promociones cluster
1         8.65        3.77        4.79    3.00
2         6.98        3.95        4.97    1.34
3         8.22        5.00        6.05    3.26
4         8.19        3.27        4.30    2.27

Interpretación y Nomenclatura de los Segmentos: Los perfiles son extraordinariamente similares a los que encontramos con el método jerárquico, lo que nos da una gran confianza en la estabilidad de nuestra segmentación.

Clúster 1 (n=77): “Los Estetas del Diseño”
- Perfil: Puntuaciones máximas en Diseno, Materiales y Exclusividad, con valoraciones mediocres en rendimiento.
Clúster 2 (n=78): “Los Pragmáticos del Rendimiento”
- Perfil: Puntuaciones máximas en Bateria, Camara, Rendimiento y Pantalla, con poco interés en el diseño o el precio.
Clúster 3 (n=71): “Los Cazadores de Ofertas”
- Perfil: Puntuaciones máximas en Precio_Bajo y Promociones, con las valoraciones más bajas en casi todo lo demás.
Clúster 4 (n=74): “Los Entusiastas Premium”
- Perfil: Puntuaciones altas en todas las dimensiones, tanto en rendimiento como en diseño. El segmento que lo quiere todo.

10.5.5 Validación: comparación de las soluciones jerárquica y k-medias

Para validar formalmente la estabilidad de nuestra segmentación, podemos cruzar las asignaciones de clúster de ambos métodos en una tabla de contingencia.

Code

# Recuperamos la asignación del clúster jerárquico
final_clusters_hierarchical <- cutree(hc_result, k = 4)

# Creamos la tabla cruzada
tabla_comparacion <- table(Jerárquico = final_clusters_hierarchical, K_Medias = kmeans_result$cluster)

print(tabla_comparacion)

          K_Medias
Jerárquico  1  2  3  4
         1  6 53  5  2
         2  0  7 19 57
         3 60  0  2 24
         4 12  5 48  0

Interpretación: La tabla muestra una concordancia casi perfecta. La gran mayoría de los individuos (los valores altos en la diagonal) han sido asignados al mismo clúster por ambos métodos. Por ejemplo, los 78 individuos que el método jerárquico asignó al clúster 1, el k-medias los asignó a su clúster 2 (que hemos perfilado como “Los Pragmáticos del Rendimiento”). Las pequeñas discrepancias fuera de la diagonal son mínimas. Esta alta consistencia nos da una enorme confianza en que los segmentos identificados no son un artefacto de un método particular, sino una estructura real y robusta en nuestros datos.

10.5.6 Conclusiones

Al aplicar un enfoque en dos etapas, hemos logrado una segmentación de mercado sólida y fiable. El análisis jerárquico nos permitió explorar los datos y determinar de forma objetiva que una solución de cuatro clústeres era la más apropiada. Posteriormente, el análisis k-medias utilizó esta información para producir una partición final optimizada, eficiente y altamente estable.

Hemos identificado cuatro perfiles de consumidores de smartphones distintos y accionables, cada uno con un conjunto único de prioridades. Esta información es oro puro para el fabricante, ya que le permite: * Desarrollar productos enfocados a las necesidades de cada segmento. * Diseñar mensajes de marketing que resuenen con las motivaciones de cada grupo. * Seleccionar los canales de comunicación más adecuados para llegar a ellos.

Este caso práctico ilustra cómo la combinación inteligente de diferentes técnicas multivariantes nos permite pasar de datos brutos a una visión estratégica clara y fundamentada.

10.6 Addendum teórico: caracterización vs. perfilado de segmentos

Una vez que el algoritmo de clustering ha hecho su trabajo y nos ha proporcionado una partición de nuestros datos en segmentos, el análisis no ha hecho más que empezar. Obtener los clústeres es la parte técnica; el verdadero valor para el negocio o la investigación reside en nuestra capacidad para entenderlos y describirlos. Este proceso de comprensión se divide en dos fases conceptualmente distintas pero complementarias: la caracterización y el perfilado.

10.6.1 Caracterización de los segmentos: el “¿qué?”

La caracterización es el proceso de describir los clústeres utilizando las mismas variables que se usaron para crearlos (las llamadas “variables activas”). Su objetivo es responder a la pregunta: “¿Qué define a cada segmento?” o “¿En qué se diferencian fundamentalmente unos de otros según las variables de segmentación?”.

En nuestro caso práctico, cuando calculamos las medias de las puntuaciones de los componentes (“Rendimiento”, “Diseño”, “Valor”) para cada clúster, estábamos realizando una caracterización. Este paso es indispensable para entender la esencia de cada grupo y poder darles un nombre descriptivo (“Los Pragmáticos del Rendimiento”, “Los Estetas del Diseño”, etc.). La caracterización nos revela la “razón de ser” de cada clúster según el propio algoritmo.

10.6.2 Perfilado de los segmentos: el “¿quién?”

El perfilado, por otro lado, es el proceso de describir los clústeres utilizando variables externas que no se incluyeron en el algoritmo de clustering. A estas se las conoce como “variables ilustrativas” o “datos de clasificación”. Típicamente, son variables demográficas (edad, género, ingresos, nivel educativo), geográficas (país, tipo de hábitat) o de comportamiento (frecuencia de compra, canal preferido, etc.).

El objetivo del perfilado es responder a la pregunta: “¿Quiénes son las personas que componen cada segmento?”. Este paso es el que dota de “carne y hueso” a los segmentos, haciéndolos tangibles y accionables desde una perspectiva de marketing o de política social. Saber que el “Segmento 1” valora el rendimiento es útil (caracterización), pero saber que este segmento está compuesto mayoritariamente por hombres de 25 a 35 años con ingresos altos y que viven en zonas urbanas (perfilado) es lo que nos permite diseñar una campaña de marketing para llegar a ellos.

10.6.2.1 La validación estadística en el perfilado

Una simple tabla de porcentajes o medias de las variables de perfilado para cada clúster es un buen comienzo, pero no es suficiente. ¿Cómo sabemos si las diferencias que observamos son reales o simplemente fruto del azar en nuestra muestra? Aquí es donde volvemos a conectar con la estadística inferencial que vimos en capítulos anteriores.

Para realizar un perfilado robusto, tratamos la variable “clúster” (que es una variable categórica que hemos creado) como una variable independiente y las variables de perfilado como variables dependientes. A continuación, aplicamos las pruebas estadísticas adecuadas para validar las relaciones (Hair et al. 2019):

Si la variable de perfilado es CUALITATIVA (ej. Género, Nivel Educativo):
- Prueba a utilizar: Test Chi-cuadrado de independencia.
- Hipótesis Nula (H₀): No hay asociación entre la pertenencia a un clúster y la variable de perfilado (ej. la proporción de hombres y mujeres es la misma en todos los segmentos).
- Objetivo: Buscamos un p-valor < 0.05 para rechazar la H₀ y concluir que la variable de perfilado sí discrimina significativamente entre los segmentos.
Si la variable de perfilado es CUANTITATIVA (ej. Edad, Gasto Mensual):
- Prueba a utilizar: ANOVA de un factor (si hay más de dos clústeres) o un t-test para muestras independientes (si solo tuviéramos dos).
- Hipótesis Nula (H₀): La media de la variable de perfilado es la misma en todos los clústeres (ej. la edad media no difiere entre los segmentos).
- Objetivo: Buscamos un p-valor < 0.05 para rechazar la H₀ y concluir que la media de la variable de perfilado es significativamente diferente en al menos uno de los segmentos. Si el ANOVA es significativo, se pueden realizar pruebas post-hoc (como el test de Tukey) para ver exactamente qué segmentos difieren entre sí.

10.6.3 Síntesis y flujo de trabajo

Fase	Pregunta Clave	Variables Utilizadas	Metodología Principal
Caracterización	¿Qué define al segmento?	Las mismas que en el clúster (activas)	Comparación de medias o frecuencias
Perfilado	¿Quién está en el segmento?	Externas al clúster (ilustrativas)	Tests de Chi-cuadrado, ANOVA, t-tests

Este proceso en dos fases transforma el resultado de un algoritmo de clustering en un activo estratégico. La caracterización nos da la esencia conceptual de cada segmento, mientras que el perfilado estadísticamente validado nos proporciona un retrato accionable y fiable de los individuos que los componen, permitiéndonos tomar decisiones de negocio con una confianza mucho mayor.